
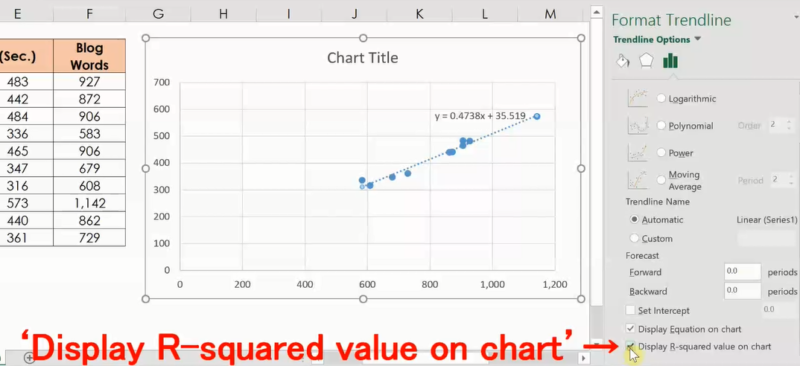
Python : Calculate Adjusted R-Squared and R-Squared In this case, adjusted r-squared value is 0.4616242 assuming we have 3 predictors and 10 observations. Let's assume you have three independent variables in this case.Īdj.r.squared = 1 - (1 - R.squared) * ((n - 1)/(n-p-1)) Print(R.squared) Final Result : R-Squared = 0.6410828 Select 'display R-squared value on chart' at the bottom.

Once you have added the trend line, click on it and a 'Format Trendline' window will appear. On the 'Chart design' ribbon, look for the button shown (Add chart element) in the picture below to add the trend line. In this example, y refers to the observed dependent variable and yhat refers to the predicted dependent variable. vamihe30 Add a trend line by selecting any data point. In the script below, we have created a sample of these values. Suppose you have actual and predicted dependent variable values. R : Calculate R-Squared and Adjusted R-Squared Adjusted R-square should be used while selecting important predictors (independent variables) for the regression model. It means third variable is insignificant to the model.Īdjusted R-square should be used to compare models with different numbers of independent variables. Whereas r-squared increases when we included third variable. It declines when third variable is added. In the table below, adjusted r-squared is maximum when we included two variables. Whereas Adjusted R-squared increases only when independent variable is significant and affects dependent variable. Every time you add a independent variable to a model, the R-squared increases, even if the independent variable is insignificant.In the above equation, df t is the degrees of freedom n– 1 of the estimate of the population variance of the dependent variable, and df e is the degrees of freedom n – p – 1 of the estimate of the underlying population error variance.Īdjusted R-squared value can be calculated based on value of r-squared, number of independent variables (predictors), total sample size.ĭifference between R-square and Adjusted R-square The only difference between R-square and Adjusted R-square equation is degree of freedom. It penalizes you for adding independent variable that do not help in predicting the dependent variable.Īdjusted R-Squared can be calculated mathematically in terms of sum of squares. It measures the proportion of variation explained by only those independent variables that really help in explaining the dependent variable.

Higher R-squared value, better the model. And a value of 0% measures zero predictive power of the model. A r-squared value of 100% means the model explains all the variation of the target variable. R-Squared is also called coefficient of determination. SSreg measures explained variation and SSres measures unexplained variation.Īs SSres + SSreg = SStot, R² = Explained variation / Total Variation In this case, SStot measures total variation. Mathematically, R-squared is calculated by dividing sum of squares of residuals ( SSres) by total sum of squares ( SStot) and then subtract it from 1. In other words, some variables do not contribute in predicting target variable. In reality, some independent variables (predictors) don't help to explain dependent (target) variable. It assumes that every independent variable in the model helps to explain variation in the dependent variable. It measures the proportion of the variation in your dependent variable explained by all of your independent variables in the model. It includes detailed theoretical and practical explanation of these two statistical metrics in R. Scores of all outputs are averaged with uniform weight.In this tutorial, we will cover the difference between r-squared and adjusted r-squared.
#Graph r squared value full#
Returns a full set of scores in case of multioutput input. multioutput, array-like of shape (n_outputs,) or None, default=’uniform_average’ĭefines aggregating of multiple output scores.Īrray-like value defines weights used to average scores.ĭefault is “uniform_average”. sample_weight array-like of shape (n_samples,), default=None y_pred array-like of shape (n_samples,) or (n_samples, n_outputs)Įstimated target values. Parameters y_true array-like of shape (n_samples,) or (n_samples, n_outputs) Note: when the prediction residuals have zero mean, the \(R^2\) score These cases are replaced with 1.0 (perfect predictions) or 0.0 (imperfect Higher-level experiments such as a grid search cross-validation, by default To prevent such non-finite numbers to pollute Is not finite: it is either NaN (perfect predictions) or -Inf
In the particular case when y_true is constant, the \(R^2\) score Non-constant, a constant model that always predicts the average yĭisregarding the input features would get a \(R^2\) score of 0.0. \(R^2\) (coefficient of determination) regression score function.īest possible score is 1.0 and it can be negative (because the r2_score ( y_true, y_pred, *, sample_weight = None, multioutput = 'uniform_average', force_finite = True ) ¶


 0 kommentar(er)
0 kommentar(er)
